Nodes or vertices connected to each other through edges.
A graph G is an ordered pair of a set of vertices V and a set of edges E.
- Ordered pair vs Unordered pair { Set}
- Directed edges(Digraph) vs Undirected Edges
- Weighted vs Unweighted edges
- Unweighted graph = Weighted graph with all weights equal
- Self-looping edges on a single vertex
- Multi-edge graphs
- Maximum number of edges in a directed graph= (n)*(n-1)
- Maximum number of edges in an undirected graph= (n)*(n-1) / 2
- Dense graph( Edges ~ (Vertices) squared) vs Sparse graph( Edges ~ (Vertices))
Path= Sequence of vertices where each adjacent vertex is connected by an edge.
A path in a graph G is a sequence of vertices v0, v1, …, vn so that for all i, (vi -> v(i+1)) is an edge of G.
Walk= A path in which vertices and edged may be repeated.
Trail= A walk in which no edges are repeated.
Simple Path= A walk in which no vertices and no edges are repeated.
Connected Graph= Path exists from any vertex to any other vertex.
Undirected graph is Connected.
Directed graph is Strongly Connected.
If directed graph is not strongly connected but can be converted to a connected(undirected) graph, it is called Weakly Connected.
Closed Walk= A walk which starts and ends at the same vertex. Length must be > 0.
Simple Cycle= No repetition of vertices other than start and end.
Acyclic Graph= Undirected Acyclic Graph = Tree, Directed Acyclic Graph= DAG
Connected Components= The vertices of a graph G can be partitioned into connected components so that v is reachable from w if and only if they are in the same connected component.
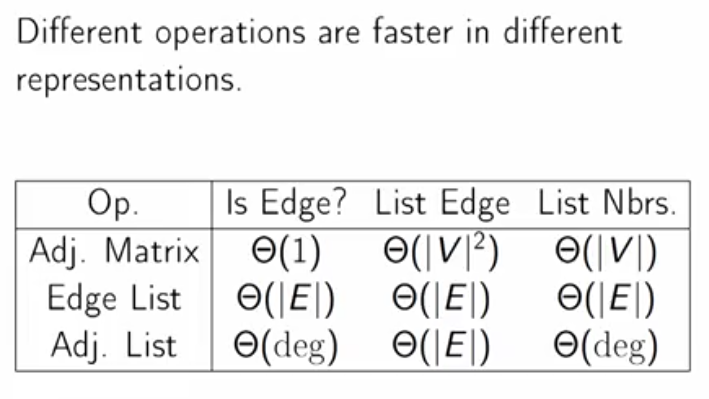
Storage of Graph
- List of all edges
- As an ordered pair of {vertex list, edge list} = O(Edges) cost
- Adjacency Matrix = O(Vertices) cost
- Useful for dense graphs
- Adjacency List= Store only those vertices which are connected
- Array / Linked List / BST
Exploring Graph
- Depth First Traversal (Stack)
- Needs adjacency list for efficient execution
- O(|E|) execution time

- Determine Connected Components


- Runtime = O(|V| + |E|)
- Determine Previsit and Postvisit numbers
- Breadth First Traversal (Queue)
